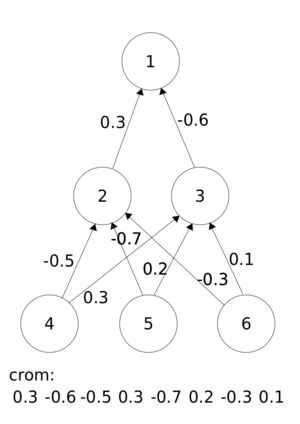
Algoritmo genético
Algoritmos genéticos (AG) são métodos de busca heurística de otimização global.[1] São utilizados na ciência da computação para achar soluções aproximadas em problemas de otimização e busca usando-se métodos inspirados na biologia evolutiva. Algoritmos genéticos são uma classe particular de algoritmos evolutivos que usam técnicas inspiradas na biologia evolutiva, como hereditariedade, mutação, seleção natural e recombinação (ou crossing over).[2] Porque eles foram inspirados na teoria da evolução, alguns evolucionistas os reivindicam como evidência de que a evolução de micróbios para humanos é possível.
Descrição
Usa-se o termo comum Computação Evolutiva para definir o ramo da ciência da computação baseado nos mecanismos evolutivos.[3] Entre seus ramos se encontra a Estratégia Evolutiva, os Programas Evolutivos e os Algoritmos Genéticos. Como por exemplo, a programação evolutiva de L. J. Fogel, a técnica de busca de dispersão de F. Glover e os algoritmos genéticos propostos por John Henry Holland[4] são programas deste ramo.
Algoritmos genéticos são implementados como uma simulação computacional na qual uma população de representações abstratas de soluções é selecionada em busca de soluções melhores. A evolução geralmente se inicia a partir de um conjunto de soluções criado aleatoriamente e é realizada por meio de gerações. A cada geração, a adaptação de cada solução na população é avaliada, alguns indivíduos são selecionados para a próxima geração, e recombinados ou mutados para formar uma nova população. A nova população então é utilizada como entrada para a próxima iteração do algoritmo.
Algoritmos genéticos diferem dos algoritmos tradicionais de otimização em basicamente quatro aspectos:
- Baseiam-se em uma codificação do conjunto das soluções possíveis, e não nos parâmetros da otimização em si;
- Os resultados são apresentados como uma população de soluções e não como uma solução única;
- Não necessitam de nenhum conhecimento derivado do problema, apenas de uma forma de avaliação do resultado;
- Usam transições probabilísticas e não regras determinísticas.[4]
A teoria tradicional dos Algoritmos Genéticos assume em um nível geral de descrição que os AG´s funcionam pela descoberta, enfatização, e recombinação de bons blocos de construção de soluções em uma maneira altamente paralela.
Algoritmo
Os Algoritmos genéticos tem em geral a forma descrita no algoritmo que se segue:
função AlgoritmoGenético()
inicializaPopulaçãoAtual() //→ cria uma lista de indivíduos, em geral de forma aleatória
avaliaIndividuosPopulaçãoAtual() //→ aplica a função-objetivo para cada indivíduo obtendo um valor
enquanto naoAtingiuCondiçãoParada() faça
lista de pais := selecionaPais() //→ seleciona-se os pais da próxima geração (por exemplo: método da roleta)
aplicaOperadorCrossingOver() //→ aplica operador de recombinação (crossing-over)
aplicaOperadorMutações() //→ gera mutações (importante para evitar picos locais)
ampliaPopulação() //→ Estende a populaçãoAtual acrescentando a populaçãoNova a ela
reduzPopulação() //→ Reduz a população estendida
avaliaIndividuosPopulaçãoAtual() //→ aplica a função-objetivo para cada indivíduo obtendo um valor
fim enquanto
retorna o melhor indivíduo da população de acordo com a função-objetivo alcançada
Representação
Os cromossomos podem ser representados de diversas maneiras. A mais comum é a representação através de uma string de bits. Outras representações podem ser cadeias de caracteres, vetores com valores inteiros ou reais (para pesos, por exemplo), listas em Lisp, etc. Outro tipo de representação (menos parecida com os casos biológicos) é a representação na forma de árvores.
Recombinação (Crossing-over)
O procedimento de recombinação depende da forma se construiu a estrutura de dados para os cromossomos.
Recombinação em um ponto
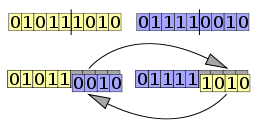
Na forma mais comum, a recombinação de um-ponto, os cromossomos são representados como uma string de bits. A descrição mais geral deste procedimento é como abaixo:
função recombinação() obtém pais() escolhe um ponto de corte // Em geral de forma aleatória troca um dos ramos do cromossomo "pai" com o do cromossomo "mãe" retorna dois novos indivíduos recombinados
Por exemplo, supondo os cromossomos:
011011010101010101011111011 (pai) e 111101001110110011011001100 (mãe)
Sorteia-se um ponto de corte (por exemplo, na posição 8) como abaixo:
01101101|0101010101011111011 (pai) e 11110100|1110110011011001100 (mãe)
trocam-se os ramos obtendo-se dois novos indivíduos:
111101000101010101011111011 (filho 1) e 011011011110110011011001100 (filho 2)
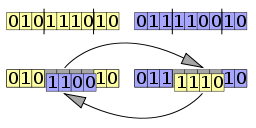
Recombinação em dois pontos
A recombinação em dois pontos seleciona duas localizações para que os cromossomos pais possam ser cortados. Todo o trecho entre esses dois pontos é trocado, resultando em dois organismos filhos diferentes:
Corte e junção
Na abordagem da recombinação "corte e junção", os pontos para o corte são selecionados de forma separada em cada um dos pais. Isso pode resultar em comprimentos diferentes dos organismos gerados.
Recombinação de Multi-pontos
Alguns AG´s permitem que o crossing over se estabeleça em mais de um trecho dos cromossomos. Nesta técnica, muitos pontos de cruzamento podem ser utilizados.
Recombinação Uniforme
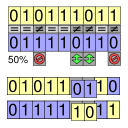
A recombinação uniforme (UX, do inglês Uniform Crossover) não utiliza pontos de cruzamento, mas determina, através de um parâmetro global, qual será a probabilidade de cada variável sofrer troca entre os pais. Nesta abordagem, os bits dos cromossomas dos progenitores se combinam para formar seus descendentes. Um a um os bits são comparados e são trocados dependendo de uma probabilidade previamente fixada, comumente 0,5.
Recombinação metade uniforme
Na abordagem da recombinação metade uniforme (HUX, do inglês Half Uniform Crossover), apenas a metade dos bits que são diferentes são trocados. Para isso, primeiro se calcula o número de bits diferentes (distância de Hamming) entre os pais. A metade desse número é o número de bits que serão trocados entre os progenitores para formar os descendentes.
Métodos de escolha para realizar a recombinação cromossômica
Para se realizar a recombinação ou crossover, dois progenitores por vez precisam ser escolhidos. Diversos métodos para esta escolha estão propostos, entre eles:
- Amostragem estocástica uniforme (Stochastic universal sampling) O indivíduo é selecionado com base em sua aptidão. A probabilidade de um indivíduo ser selecionado aumenta proporcionalmente à medida de sua aptidão em relação aos demais candidatos a progenitor. Os indivíduos são mapeados em segmentos contíguos de uma reta proporcionais à sua aptidão.
- Método da Roleta (Roulette wheel selection) (SCX) Também é conhecido como seleção proporcional à aptidão (Fitness-Proportionate Selection). O indivíduo é selecionado com base em sua aptidão. A probabilidade de um indivíduo ser selecionado aumenta proporcionalmente à medida de sua aptidão em relação aos demais candidatos a progenitor. Difere da amostragem estocástica uniforme simplesmente por ser em uma roleta viciada ao invés de uma reta.
- Seleção Boltzmann (Boltzmann selection) Estabelece uma pressão de seleção variável de acordo com o tempo da pesquisa de solução. Inicialmente, permite a reprodução de indivíduos com baixa aptidão de modo a manter a diversidade da população e evitar convergências prematuras. Com o tempo, vai aumentando a pressão seletiva de modo a favorecer cada vez mais os indivíduos com aptidão mais alta.[5]
- Método do Torneio (Tournament selection) Consite em selecionar uma série de indivíduos da população e fazer com que eles entrem em competição pelo direito de ser um dos progenitores.
- Seleção por ranking (Rank selection)
- Seleção Truncada (Truncation selection)
- Steady state selection
- Seleção local (Local selection)
Mutação
O mecanismo de mutação não é necessário para que os AG's consigam resolver diversos problemas.[6] Contudo, as mutações são um mecanismo útil que pode ser usado para o contorno de picos locais. Atualmente a mutação é um mecanismo amplamente usado, especialmente em aplicações de modelagem.
Operadores de Mutação
Existem muitos operadores de mutação em uso. Alguns são exemplificados abaixo:
- Mutação de subárvores - substitui uma subárvore selecionada por uma gerada aleatóriamente.
- Mutação de subárvores de tamanhos equitativos - substitui uma subárvore selecionada por uma gerada aleatóriamente, mas de tamanho equivalente a árvore substituída.
- Mutação pontual - substitui um ponto aleatóriamente.
- Mutação guindaste - cria uma nova prole que é uma cópia de uma subárvore do pai escolhida aleatóriamente.
Mutações inspiradas na biologia
Alguns dos mecanismos de mutação se inspiram nas mutações e erros de cópia que ocorrem naturalmente. Alguns são exemplificados abaixo:
- Mutação por inversão - processo no qual a informação em um gene é invertida.[7]
- Mutação por permutação - processo no qual a informação de mais de um gene é trocada entre si. Permuta os elementos.
Frequência das Mutações
A frequência das mutações também é um parâmetro a ser considerado. Alguns AGs permitem que se configure o percentual de mutações. A probabilidade em geral deve ser baixa (< 10%) para que o algoritmo não perca a característica de estar relacionado com os sucessos obtidos pelos seus ascendentes e não tenda a se tornar uma busca aleatória.
Propósito e Limites
Embora alguns evolucionistas afirmam que os algoritmos genéticos são uma evidência de que a evolução do micróbio para o homem é possível, as reivindicações são falhas em vários pontos.
- Algoritmos genéticos muitas vezes começam com um conjunto de "genes" aleatórios. No mundo real, um organismo com genes aleatórios não viveria. Por outro lado, quando os algoritmos genéticos já começam com uma solução viável e funcional isto não se encaixa no quadro da teoria da evolução, que alegadamente começa a partir de aminoácidos que foram formados em um tipo de sopa primordial. No segundo caso, isto se parece mais com o modelo criacionista pois os tipos iniciais aparecem já prontos.
- Algoritmos genéticos não têm passos fatais[nota 1]. No mundo real os genes são códigos de instrução complexos tais que a combinação de dois intermediários entre dois estados viáveis muitas vezes pode ser fatal. É muito parecido com um programa de computador, que tem comandos discretos, mas tentando ir de um comando para outro um bit de cada vez irá fará com que o programa deixe de funcionar.
- Algoritmos genéticos colocam as instruções para funções críticas, tais como a reprodução além da influência das mutações, de modo que as mutações não perturbam essas funções. No mundo real funções críticas muitas vezes podem ser destruída por mutações.
- Os algoritmos genéticos nunca produzem novas capacidades além das que são pré-programadas para eles. A evolução do micróbio ao homem capacidades totalmente novas e complexas a serem desenvolvidas muitas e muitas vezes.
- Os algoritmos genéticos começam com processos totalmente funcionais projetados para eles. Os a evolução do micróbio para o homem exige que esses processos sejam desenvolvidos a partir do zero, mas eles são necessários para a vida. Ou seja, o primeiro salto (da matéria inanimada ao primeiro micróbio capaz de perfazer as funções básicas como comer, crescer e se reproduzir) deve ser feito em um passo único.
- Os algoritmos genéticos são concebidos por programadores inteligentes, com um problema específico em mente e totalmente funcionais desde o início. Para corretamente imitar a evolução biológica, os "organismos" iriam precisar de:
- Os "organismos" teriam que ser um programa já totalmente funcional, com uma linguagem de programação detalhada que lhe diga como fazer cada coisa.
- Os organismos teriam de desenvolver a linguagem de programação a partir do zero, sem auxílio de um programador.
- Os organismos teriam que desenvolver o sistema operacional inteiro do zero, sem auxílio de um programador.
- Os organismos teriam que desenvolver um sistema para ler e escrever as instruções de programação também a partir do zero, sem auxílio de um agente inteligente.
- Os organismos teriam de desenvolver e construir a memória do computador e o processador a partir do zero, sem auxílio de um agente inteligente.
- Os algoritmos genéticos têm uma definição restrita de fitness. O "fitness" do "organismo" é medido com base em quão bem se encaixa em um problema específico. No mundo real os organismos ou vivem ou morrem. Se viverem o tempo suficiente, eles costumam se reproduzir. De acordo com a Wikipédia em inglês este é um tipo de problema que os algoritmos genéticos (AGs) não podem efetivamente resolver.
| “ | Os AGs não podem efetivamente resolver problemas em que não há maneira de julgar a aptidão de uma resposta que não seja certa/errada, se não há nenhuma maneira de convergir para a solução. Estes problemas são freqüentemente chamados de problemas "agulha no palheiro" "(needle in a haystack)".[8] | ” |
Embora alguns evolucionistas afirmem que os algoritmos genéticos são uma evidência de que a evolução do micróbio para o homem seja possível, é evidente que eles não representam adequadamente a biologia e nada mostra, como tal, sobre a plausibilidade desta evolução do micróbio para o homem.
Exemplo Evolucionista Popular
Um exemplo citado pelos evolucionistas é uma programa de "vida artificial" chamado Avida[9]. Apesar das alegações sobre esse programa, ele não chegar nem perto de mostrar a possibilidade da evolução do micróbio para o homem. Uma falha é que cada bit do "genoma"[10] torna-se um comando completo, e que está codificado fora do genoma, o que não se encaixa nos genomas dos organismos reais. Segundo Meyer, o programa Avida não simula como a informação necessária para produzir o primeiro organismo possa ter originado.[11]
Ao contrário da maioria dos programas de algoritmos genéticos o Avida[9] inclui dois comandos de reprodução, como parte de seu "genoma"[10]mas eles só dizem o "organismo" quando se reproduzir e de que modo (sexuado ou assexuado) se usar. Em ambos os casos as instruções reais estão fora do "genoma"[10] e são, portanto, imunes à mutação. Isto permite uma mutação que torna um "organismo" estéril, mas nenhuma mutação altera as instruções pré-programadas dentro de cada comando.
Esses "organismos artificiais" não desenvolvem novas habilidades, que não são projetadas para o programa, mas simplesmente reorganizam habilidades existentes. O Avida[9] começa com uma espécie criada de "organismo" e apenas produz variedades desse organismo, em perfeito acordo com a ciência criacionista.
Alguns AG realmente não mimetizam a natureza
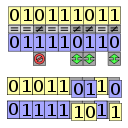
Muitos problemas para os quais a técnica de algoritmos genéticos pode ser utilizada têm um problema típico em relação à operação de cruzamento: elementos de um cromossoma podem aparecer em uma ordem diferente, mas devem ser o mesmo conjunto de elementos. Um exemplo típico disto é a utilização dos AG para resolver o problema do caixeiro viajante. Embora a ordem das cidades visitadas possa variar, todas as cidades devem ser visitadas. Em um cruzamento normal, os filhos gerados por cada conjunto de pais muitas vezes acaba com as cidades duplicadas enquanto algumas cidades não permanecem na lista. Um exemplo pode ser visto na figura abaixo. Os dois pais (p1 e p2) geram dois cromossomos filhos (o1 e o2). Neste exemplo, o cromossoma o1 carece dos elementos 3, 5 e 7, tendo os elementos 1, 6 e 9 duplicados. O cromossomo o2 carece dos elementos 1, 6 e 9, tendo os 3 elementos, 5 e 7 duplicados.
Para resolver problema como este diversas variações de cruzamento têm sido desenvolvidas. São apresentados dois exemplos que mantêm os elementos do conjunto: os cruzamentos PMX e OX. Existem outros métodos (por exemplo, o cycle crossover CX, o order-based crossover OBX, o position-based crossover PBX, o subtour exchange crossover, o heuristic crossover), mas para efeitos do presente artigo não serão discutidos aqui.
Partialy-mapped crossover (PMX)
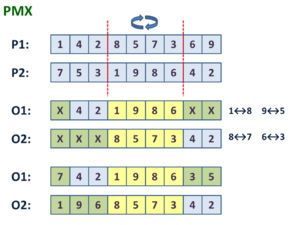
O PMX constrói uma prole escolhendo uma subseqüência de uma turnê de um dos pais preservando a ordem e a posição de tantas posições quanto possíveis do outro progenitor.[12] Em primeiro lugar, uma subsequência é delimitada por dois pontos de corte. Depois disso, os segmentos entre os pontos de corte são trocados (as posições em amarelo). Extrai-se do segmento que foi trocado uma série de mapeamentos. No exemplo apresentado: 1⇒8, 9⇒5, 8⇒7 e 6⇒3. O segundo passo é preencher as posições para as quais não há conflito. No exemplo mostrado, as posições 4 e 2 em ambos os cromossomas (as posições em azul). O terceiro e último passo é usar os mapeamentos para preencher as posições restantes (as posições em verde). Note que usando o mapeamento 1⇒8 no vetor O1 ocorre um conflito de novo de modo que se deve prosseguir usando o mapeamento 8⇒7 de modo a se obter um número não repetido.
Order crossover (OX)
O crossover OX constrói uma prole escolhendo uma subseqüência de uma turnê de um dos pais preservando a ordem relativa das posições do outro progenitor.[12] Usando o mesmo exemplo do algoritmo anterior, se corta a sequência em dois pontos. A partir do segundo ponto de um dos pais as posições do outro pai são copiadas na mesma ordem, desconsiderando-se os símbolos que já estão presentes. Atingindo o fim da cadeia, se prossegue a partir do início da cadeia. No exemplo acima, se preenche o cromossoma O2 seguindo a sequência 6⇒9⇒1⇒4⇒2⇒8⇒5⇒7⇒3 e preenchendo as posições ainda não estão presentes. São preenchidas as posições mostradas em vermelho: 4,2,5,7 e 3. Se faz o mesmo para o cromossomo o1 seguindo a lista 4⇒2⇒7⇒5⇒3⇒1⇒9⇒8⇒6 e preenchendo os posições que ainda não estão presentes. São preenchidas as posições mostradas em vermelho: 4,2,1,9 e 6.
Quadrados mágicos
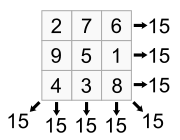
Outro exemplo de algoritmo genético que precisa ser adaptado de forma diversa do que ocorre na natureza é o problema de se encontrar um quadrado mágico de lado n. De acordo com Tao Xie e Lishan Kang, um algoritmo evolutivo simples dificilmente alcança sucesso em obter quadrados mágicos com lados maiores que 10, e a eficiência da evolução e a taxa de sucesso são extremamente baixas.[13] O que os autores propuseram em seu artigo para alcançar sucesso na geração de quadrados mágicos foi um algoritmo genético em duas etapas, a segunda com heurísticas destinadas a não destruir a soma obtida nas colunas e linhas no passo anterior, novamente de forma diversa do que ocorre na natureza.[13]
Conclusão
Os crossovers PMX e OX são feitos para lidar com o problema colocado no início desta secção. Eles resolvem bem o problema evitando valores duplicados ou ausentes. Mas este mecanismo de crossover não é encontrado em células. O crossover encontrado nas células não tem mecanismos que preservam a mesma informação em ordem diferente tais como estes. Assim, estes exemplos não podem ser utilizados para apoiar as reivindicações dos evolucionistas no que diz respeito à construção de novas informações. Se o problema do caixeiro viajante fosse resolvido com AG usando o crossover encontrado na natureza poderia nunca convergir para uma solução. Ou poderia levar um tempo grande comparável as tentativas aleatórias. Outros exemplos de AG que usam heurísticas diferentes da natureza incluem os AG para a obtenção de quadrados mágicos.
Notas
- ↑ É possível, embora não usual, se gerar uma função de fitness que resulte num valor zerado ou negativo para formas indesejáveis e que os indivíduos que tem tais valores possam nunca ser escolhidos como pais (por exemplo pelo método da roleta ou outro). Além disto, para se representar o que ocorre na natureza, o número de formas deletéreas deveria ser excessivamente grande inviabilizando o algoritmo, seja em convergência, seja em tempo de execução.
Referências
- ↑ Linden, Ricardo. Algoritmos Genéticos: Uma Importante Ferramenta da Inteligência Computacional. 2ª ed. São Paulo: Brasport, 2006. 348 p. p. 40. ISBN 85-7452-265-1
- ↑ In: Lawrence Davis. Handbook of Genetic Algorithms. New York: Van Nostrand Reinhold, 1991. p. 2. ISBN 0-442-00173-8
- ↑ Bittencourt, Guilherme. Inteligência Artificial: Ferramentas e Teorias. Florianópolis: Editora da UFSC, 2001. 362 p. ISBN 85-328-0138-2
- ↑ 4,0 4,1 Goldberg, David E.. Genetic Algorithms: in Search, Optimization, and Machine Learning. Reading, Massachusetts: Addison-Wesley, 1989. 412 p. p. 1-7. ISBN 0-201-15767-5
- ↑ Ichihara, Jorge de Araújo. Capítulo III:Algoritmos genéticos. Página visitada em 2 de novembro de 2012.
- ↑ Poli, Riccardo; Langdon, William B.; McPhee, Nicholas F.; Koza, John R. (contribuidor). A Field Guide to Genetic Programming. Estados Unidos da América: Publicado pelos autores, 2008. 233 p. p. 42-43. ISBN 978-1-4092-0073-4
- ↑ Uma Introdução aos Algoritmos Genéticos - Parte 2. Página visitada em 3 de Maio de 2012.
- ↑ Genetic algorithm. Wikipedia (en). Página visitada em 3 de Maio de 2012.
- ↑ 9,0 9,1 9,2 Avida: The Digital Life Platform. Michigan State University. Página visitada em 16 de Março de 2011..
- ↑ 10,0 10,1 10,2 A guided tour of an ancestor and its hardware. Avida: The Digital Life Platform, Michigan State University. Página visitada em 16 de Março de 2011..
- ↑ Meyer, Stephen C. Signature in the Cell: DNA and the Evidence for Intelligenct Design. New York: HarperCollins Publishers, 2009. p. 289. ISBN 978-0-06-147278-7
- ↑ 12,0 12,1 Mitchell, Melaine. An Introduction to Genetic Algorithms. Cambridge, Massachusetts: The MIT Press, 2001. p. 216-220. ISBN 0-262-63185-7
- ↑ 13,0 13,1 Xie, Tao; Kang, Lishan. (8-12 Dezembro de 2003). "An evolutionary algorithm for magic squares". Evolutionary Computation, 2003. CEC '03. 2 pp. 906-913. Changsha, China: Coll. of Comput. Sci., Nat. Univ. of Defense Technol.. DOI:10.1109/CEC.2003.1299763.
Ligações externas
- Algoritmo genético na Wikipédia
- GA Playground (Genetic Algorithms Toolkit)
- Algoritmos genéticos - eles mostram que a evolução funciona?
- The Digital Life Lab at Caltech
- Avida, um Modelo Biologicamente irreal para a Teoria Neo-darwinista
- Evolução por Design Inteligente: Uma Resposta a Lenski et al.
| |||||||||||||||||