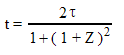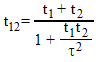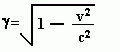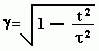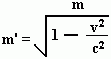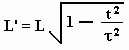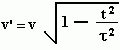Cosmological relativity
Cosmological relativity is an extension of the principles of Special and General Relativity to cosmological scales. Developed by Dr Moshe Carmeli, this theory is a combination of Einstein's original special and general relativity; however its starting point is the expansion of the Universe and not the propagation of light. It has profound results for cosmology in general and in particular Young Earth Creation cosmology. So far this theory fits all experimental findings.
Cosmic Time
Cosmic time is the time that the universe would need to expand from a zero size point for a given red shift. In the Big Bang cosmology it would be the time since the Big Bang. In any cosmology that starts with the universe as larger than a point, the universe would actually be younger than cosmic time.
- t = Cosmic time.
- z= Red Shift.
- τ = Observed Cosmic time = 13.56 Gyr.
According to Cosmological Relativity τ is constant for all space and time such that at any place in the Universe and at any time in its history an observer would measure the same Current cosmic time. Also like Einsteinian Relativity the laws of nature are the same for all space and time. The result is that there is no absolute cosmic time; instead it is relative to the time and place of the observer just like velocity in Special relativity. Also like velocity in Special relativity cosmic time does not simply add from one observer to another. Instead cosmic time is added by the following formula:
- t = Cosmic time.
- τ = Observed Cosmic time = 13.56 Gyr.
The key to Cosmological Relativity is that there is no absolute cosmic time, although any observer at any point in space and at any time will see τ = 13.56 Gyr.
5D cosmology
Cosmological relativity’s line element for an expanding Universe in negligible gravity is:
ds2 = τ2dν2 - ( dx2 + dy2 + dz2 )
- τ = H0-1 = Observed Cosmic time = 13.56 Gyr.
- H0 = Hubble’s constant.
- ν = Is the space velocity at a given point in space.
- x,y,z = Normal 3d spatial dimensions.
This is similar to the Special relativity line element.
ds2 = c2dt2 - ( dx2 + dy2 + dz2 )
- t = time.
- c = the speed of light.
- x,y,z = Normal 3d spatial dimensions.
When time is added to Cosmological relativity’s line element we get:
ds2 = τ2dν2 - ( dx2 + dy2 + dz2 ) + c2dt2
- τ = H0-1 = Observed Cosmic time = 13.56 Gyr.
- H0 = Hubble’s constant.
- ν = Is the space velocity at a given point in space.
- t = time.
- c = the speed of light.
- x,y,z = Normal 3d spatial dimensions.
The result is a theory of 5 dimensions.
- 1 of time.
- 1 of spatial expansion velocity.
- 3 normal spatial dimensions.
Special Relativity
Cosmological Special Relativity has much in common with Einstein’s Special relativity. Both theories deal with the special case of no gravity forming the basis for the more general concept. The main difference is that cosmic time (t) replaces velocity (v) as the critical quantity and observed cosmic time (τ= 13.56 Gyr) replaces the velocity of light (c) as the constant. Both theories have essentially the same formulae, but Cosmological Special Relativity substitutes ”t” for “v” and “τ” for “c”.
In Cosmological Special Relativity τ = H0-1 = 13.56 Gyr, where H0 = Hubble’s constant.
Thus both theories have similar transformations between reference frames.
- Cosmological Special Relativity
Thus both theories have similar formulae for relative mass. (m)
- Cosmological Special Relativity
Similar formulae for relative length. (L)
- Cosmological Special Relativity.
It is in the area of time (t) and velocity (v) that the two theories are the most different, since they basically switch places. However, in Cosmological Special Relativity, the velocity referred to is the expansion of the universe and not the independent motion of the object.
- Cosmological Special Relativity.
In Cosmological Special Relativity we get an added relationship for the acceleration (a) of the expansion of the universe.
Cosmological Special Relativity also has relativistic formulae for the universes’ density (ρ) and temperature (T).
Even though both the universe's density (ρ) and its temperature (T) are shown to be larger in the past, it seems likely that these are purely relativistic affects and that at those times the measured values would be what they are today.
Cosmological Special Relativity and Special relativity are not exclusive but work together, each being most significant under the right circumstances. Special relativity as v approaches c and Cosmological Special Relativity as t approaches τ.
General Relativity
Cosmological General Relativity, like Einstein’s General relativity, deals with the general case where gravity is present.
4D
In its 4D form of space-velocity, Cosmological General Relativity gives only the state of the universe in an instant of time.
While in Cosmological Special Relativity τ = H0-1, when gravity is considered as it is in Cosmological General Relativity, τ = h-1, and its relationship H0 becomes:
- Ωm =ρm/ρc = Cosmological General Relativity’s ratio of the mass density of the universe and the mass density that would result in a constant expansion rate.
- ρc = 3h2/8πG = 3/8πGτ2 = Cosmological General Relativity’s mass density at which a constant expansion rate occurs.
- ρm = measured mass density of the universe.
- z = ν /c = redshift.
- h = τ-1 = 72.17 km / s Mpc
- τ = Observed Cosmic time = 13.58 Gyr.
- G = Gravitational Constant
According to Cosmological General Relativity, the presence of gravity resulting from matter and energy reduces the vacuum pressure that tends to accelerate the expansion of the universe. This vacuum pressure (p) is denoted by:
As a result, the value of Ωm affects the expansion of the universe:
Ωm > 1
- This results in a decelerating expansion.
Ωm = 1
- This results in a constant expansion.
Ωm < 1
- This results in an accelerating expansion.
- Ωm = 0.245
When this is applied to the unbounded universe of the Big bang, the result is that for the first 5.08 Gyr after the Big bang there would be a decelerating expansion. At this point the expansion becomes constant for a brief time and then starts to accelerate as it is today.
Next we have ΩT which denotes the curvature of space on cosmic scales. The difference between ΩT and Ωm is ΩΛ. Such that:
ΩT = Ωm + ΩΛ
Now ΩΛ = (H0 / h)2 = 0.764
The result is: ΩT = Ωm + ΩΛ = 0.245 + 0.764 = 1.009 ≈ 1
This shows that the universe is flat ( Euclidean ) on a large scale
5D
When the time dimension is added to Cosmological General Relativity, the result is a 5D theory that reproduces all of the results of General Relativity with additional effects that solve a number of problems in cosmology. It results in a 5D space – time – velocity manifold that is an extension of General Relativity for cosmology.
Accelerating expansion
While the discovery of the acceleration of the expansion of the universe was a surprise to most scientists, it was actually predicted by Cosmological General Relativity. This means that Cosmological General Relativity has made a successful prediction which is important to any scientific theory. The success of this prediction should have brought attention to Cosmological Relativity, but instead current theory was simply patched with a mysterious unobserved substance called dark energy.
Galactic Rotation

In this diagram “A” is the typical rotation curve of a spiral galaxy as predicted by the established principle of gravitational mechanics. However “B” is what is actually observed.
Dr. John G. Hartnett has shown that Cosmological General Relativity naturally produces the observed curve “B”. It is a result of adding the extra velocity. As a result the rotation curve of spiral galaxies is exactly what Cosmological General Relativity says they should be.
Here is yet another case where Cosmological Relativity is shown to fit reality better than current theory. Such results are strong evidence in support of the theory.
This is a good example of how the general scientific community has to be dragged kicking and screaming to radically new concepts. Cosmological Relativity fits the data so well that it deserve serious consideration but the general scientific community prefers to keep patching existing theory.
Dark Matter
Cosmological Relativity successfully accounts for two phenomena that cosmologists have often invoked so called dark matter to explain: the rotational curves of spiral galaxies and gravitational lensing. The result is that Cosmological Relativity essentially eliminates any need for so called dark matter.
Dark Energy
Cosmological Relativity totally eliminates the need for dark energy since the accelerating expansion is an intrinsic part of its 5D space – time – velocity manifold.
Bounded Universe
Dr. John G. Hartnett has applied Cosmological relativity to a bounded universe. Under General relativity the gravity potential of a bounded universe would induce a large scale curvature to space for which there is no evidence. He found that, due to the accelerating expansion, Cosmological relativity would eliminate this curvature, making space as flat as it would be in an unbounded universe. This would be true as long as the radius ( r ) was at least cτ.
- Infinity > r ≥ cτ
He showed that observations are consistent with a bounded universe inside a white hole with our galaxy at or near the center. This is not to be confused with Dr Humphreys’ White hole cosmology since in Hartnett's model the universe is still inside the white hole’s event horizon. However there are similarities in the two cosmologies.
Young Earth Cosmology
Dr. John G. Hartnett has shown that Cosmological relativity is observationally consistent with a finite bounded universe. He has since shown that the 5D Cosmological relativistic line element shows that the universe is young by Earth clocks and that light from the most distant stars could have arrived at the Earth within the Creation week.
5D line element
ds2 = τ2dν2 - ( dx2 + dy2 + dz2 ) + c2dt2
Starting with this line element, Hartnett shows that the gamma functions of both Special relativity (λE)and Cosmological Special relativity (λc) can each be derived.
When deriving the gamma function of Special relativity the result is:
This shows that Special relativistic affects are greatly affected by the acceleration of the expansion of the universe. In fact as dν/dt approaches 0 it becomes:
This is the standard Special relativistic gamma function.
The result is that Special relativity is most accurate when the universe’s expansion is not accelerating. This suggests that today the universe either expanding at a constant rate or not at all.
When deriving the gamma function of Cosmological Special relativity the result is:
This shows that Cosmological Special relativistic effects are greatly affected by the acceleration of the expansion of the universe. In fact as dν/dt get larger it becomes:
This is the standard Cosmological Special relativistic gamma function. Based on the above 5D line element, a dν = 0 the Cosmological Special relativistic gamma function would not be in effect and the Special relativistic gamma function would function in its original form.
The result is that Cosmological Special relativity is most accurate when the universe’s expansion is accelerating very fast. This suggests that in the past the universe had a period of rapidly accelerating expansion.
Combined, these results show that at some time in the past the universe experienced a rapidly accelerating expansion but that today the expansion is either constant or has stopped. It also tilts the observational evidence from being neutral towards favoring a bounded over an unbounded universe. Such a rapidly accelerating expansion would have left clear observational evidence in an unbounded universe because, without a center, time dilation would not make local expansion rates seem slower than would be seen at the center. The time dilation effect at the center relative to any distance from the center would be:
- dt = time at the center.
- dT= time at point commoving with the expansion
With a velocity v = 0 the relationship becomes:
- dt = time at the center.
- dT= time at point commoving with the expansion.
Observation shows that in a bounded universe the Earth would be near the center. So based on the Biblical account, it is likely that the Earth was at the center of the expansion.
Since the rapid acceleration of the universe’s expansion has stopped, Earth’s time is now approximately the same as time in the rest of the universe, thus there is no blue shift as would be expected as a result of time dilation.
It is theorized that during the first few days of creation the universe had a period of rapidly accelerating expansion, resulting in a high degree of time dilation on Earth. This concept is similar to Dr Humphreys’ White hole cosmology but it lacks the gravitational distortion of a massive white hole.
One way light travel time to Earth
Hartnett has worked out a relationship between the distance from Earth and the acceleration of the expansion of the universe in the form of an exponential function which demonstrates that the one way light travel time to Earth could easily have been no more than a few days in Earth time and even possibly less than one day. The exact time depends on the exact acceleration rate.
- τ = Observed Cosmic time = 13.56 Gyr
- c = Speed of light.
- r = The distance from the center.
- t =The one way light travel time to Earth in Earth time.
- η = A proportionality constant.
The following graph shows the results for various distances (r) with η set to two different values.
Note that at η = 1013 that the light even from 13.56 billion ly would have reached Earth in about a day.
While these results are not exact they do show that Cosmological relativity in a bounded universe can get even the most distant star light possible to Earth within the creation week. The result is that Hartnett’s cosmology is a viable young Earth cosmology.
Conclusion
While Cosmological relativity is not yet generally accepted, it is a viable theory of physics that has already been shown to naturally explain several problems in cosmology, including some it was not developed to explain.
It also results in a viable young Earth cosmology when applied to a bounded universe.
Related References
Dr. Moshe Carmeli
- Accelerating Universe, Cosmological Constant and Dark Energy
- Accelerating Universe: Theory versus Experiment
- Aspects of Cosmological Relativity
- The Cosmic Time in Terms of the Redshift
- Cosmological Relativity: A General-Relativistic Theory for the Accelerating Expanding Universe
- Cosmological Relativity: A New Theory of Cosmology
- Cosmological Relativity: Determining the Universe by the Cosmological Redshift
- Cosmological Relativity: The Special and General Theories of the Structure of the Universe
- Cosmological Special Relativity: The Large-Scale Structure of Space, Time and Velocity
- Cosmological Theories of Special and General Relativity - I
- Cosmological Theories of Special and General Relativity - II
- Derivation of the Tully-Fisher Law from General Relativity Theory: Doubts about the Existence of Halo Dark Matter
- Is Galaxy Dark Matter a Property of Spacetime?
- Five-Dimrnsional Cosmological Theory of Unified Space, Time and Velocity
- Five-Dimensional Brane World Theory
- Fundamental Approach to the Cosmological Constant Issue
- The Line Elements in the Hubble Expansion
- Value of the Cosmological Constant: Theory versus Experiment
- Velocity, Acceleration and Cosmic Distances in Cosmological Special Relativity
Dr. John G. Hartnett
- Starlight, Time and the New Physics
- Carmeli's cosmology fits data for an accelerating and decelerating universe without dark matter nor dark energy
- Carmeli's accelerating universe is spatially flat without dark matter
- The Carmeli metric correctly describes spiral galaxy rotation curves
- The distance modulus determined from Carmeli's cosmology fits the accelerating universe data of the high-redshift type Ia supernovae without dark matter
- A 5D spherically symmetric expanding universe is young
- Finite bounded expanding white hole universe without dark matter
- Properties of gravitational waves in Cosmological General Relativity
- Spiral galaxy rotation curves determined from Carmelian general relativity
- Welcome to John Hartnett's Home Page
Carmeli & Hartnett
| |||||||||||