Moon recession
Moon recession is the phenomena whereby the moon is receding (moving away from) the Earth at a measurable rate. Based on current measurements and estimates the moon would have been in contact with Earth approximately 1.2 billion years ago. This recession is young solar system evidence, which puts an upper limit on the age of the Earth / Moon system as being much younger than the 4.6 billion years it is normally estimated to be.
The Earth and Moon Relationship
The distance between the Earth and the Moon is about 384,000 km. (2. 239,000 miles) Due to tidal forces it is getting farther from the Earth at a rate of about 3.8 cm/yr. (1.5 inches/yr)
This occurs because Moon’s gravity causes a small bulge in the Earth, and because of Earth’s rotation this bulge leads the Moon. As a result the Moon pulls on the bulge against Earth’s rotation. This speeds up the Moon, while slowing the Earth rotation.
Gravitational-rotational relationship
The current rate of slowing of the Earth rotation rate is about 8.836 milliseconds / year. This is often mistakenly projected back in a straight line but physics shows that rate would be higher when the Moon was closer. There are two factors that cause the moon's recession rate to be faster in the past.
- A faster rotation rate for the Earth causes the tidal bulge's lead on the Moon to be larger, and this increases the net tidal force, which causes the moon to recede faster.
- The inverse square law. Simply put the force of gravity changes with the square of the distance, such that if the distance is reduced by 1/2 the force of gravity increases by a factor of four.
Forming an equation
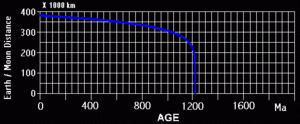
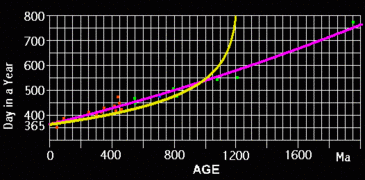
We start with a measured lunar recession rate of 3.82 cm/yr, and the measured slowing of the Earth's rotation rate of 8.812 milliseconds /year/year. If you plug these values into the laws of physics you get the following charts of the number of days in a year and Earth/Moon distance.
Note that it climbs sharply as it nears the 1.2 billion year mark. This is because if the moon is closer the tidal forces are greater and the slow down rate is greater.
When this projection is carried out for the moon's distance from the Earth it turns out that the moon's recession rate would have been much faster than its current 3.82 cm/yr, such that it would have been at the Earth's surface just 1.1832 billion years ago. That's about 3.4 billion years too recent for uniformitarian geology.
Old Earth Arguments
One argument used to save the old Earth model is that continental location affects tidal drag. While this is true since the closer the Moon the stronger its pull on the Earth the rate of change tends to get very large. The result is that to save the old Earth model it becomes necessary to virtually eliminate the effect of the continents.
Eugene Poliakow's paper “Numerical modelling of the paleotidal evolution of the Earth-Moon System” is an example of efforts to calculate the effect of continental movement based on actual estimates of past continental movement. Because of limitations of the methods used to estimate past continental movement, it only projects back 600 million years, but this is enough to evaluate the results.
The following chart shows the results.
| Time before now in millions of years | Lunar recession in cm/year | Earth's rotation slowing in seconds/century |
|---|---|---|
| 0 | 2.91 | 1.59 |
| 10 | 2.68 | 1.46 |
| 50 | 1.83 | 0.98 |
| 100 | 0.81 | 0.43 |
| 200 | 0.34 | 0.18 |
| 300 | 0.46 | 0.24 |
| 350 | 0.80 | 0.42 |
| 400 | 0.57 | 0.30 |
| 450 | 1.54 | 0.80 |
| 500 | 2.53 | 1.31 |
| 570 | 2.19 | 1.11 |
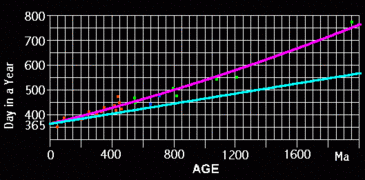
The way to judge the validity of a mathematical model is to see how well it reproduces known data. Poliakow’s calculations give (as seen in the above chart) a figure of 2.91 cm/yr as the Moon’s current recession rate and 1.59 seconds /year/century as the rate of slowing of Earth’s rotation. The problem with these figures is that they both differ significantly from the values actually observed. The Moon’s current recession rate has actually been measured at 3.82 cm/yr, which is nearly one third larger than Poliakow’s model indicates. Furthermore the slowing of Earth’s rotation has been measured at 0.8812 seconds /year/century which is just 55% of what Poliakow’s model indicates.
At first glance the fact that Poliakow’s model overestimates the deceleration rate of Earth’s rotation would seem to be a plus, however the limiting factor of the age of the Earth - Moon system is the position of the Moon, not the Earth rotation rate. Since the Moon’s recession rate is actually higher than in Poliakow’s model, the error would be a clear negative. The real problem is that discrepancies between the model and real world data show there to be a fundamental flaw in the model. It means that Poliakow overlooked one or more major factors that could easily nullify his results.
The other flaw in this model is that it does not produce results consistent with paleontological evidence. Any old Earth model for evolution of the Earth – Moon system would have to agree with both present system data and paleontological evidence, but Poliakow’s model disagrees with both.
- Made from data at Impact origin of the moon
There is paleontological evidence claimed as independent evidence for an old Earth, but like any other dating method this interpretation assumes conditions similar today, while ignoring the potential affect of a global flood on the data. This claim is based on the fact that tidal forces from the Moon are slowing the Earth rotation rate.
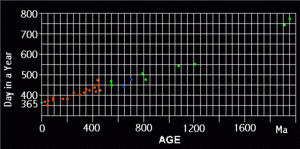
It is claimed that stromatolites, fossil tidal rhythmites, and fossil bivalves and coral all have growth indicators showing more days in a year at the time when they lived. However when one looks closely at this data, the claim is shown not to be valid.
The first clue is the degree of scattering in the data. It is not what would be expected if it were really the result of lunar recession. It should produce a clear curve but it does not. Now scattering often occurs in data, but in this case there is no reason for the scattering, if the differences were a result of the slowing of the Earth rotation rate. This is because the rate of change would be too slow to cause scattering, if the data was actually a result of the number of days per year. Furthermore when other studies are considered, they show the degree of scattering is actually higher than is shown here.
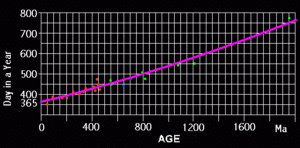
When a statistical curve fit is graphed to this data; (the purple line) you see that it does not agree with any mathematical model.
Not only does it suggest a faster rate of change than what is actually observed, but also faster than what would allow the Earth-Moon system to last 4.5 billion years. It suggests a rate faster than predicted or allowed for by any known mathematical model, and probably faster than any physically possible model.
The result is that when paleontological data is compared to real tidal force data it shows that it is not what is predicted by an old age model. However if the data results from factors other than the Earth's rotation rate, such as long lived bivalves and coral and hydrological sorting, then the degree of scatter makes sense. As a result, paleontological data is actually more consistent with a young created Earth and a global flood than an old Earth.
See Also
- Moon is receding at a rate too fast for an old universe Response to Talk.Origins
References
- Our Created Moon book by Don DeYoung
- Young age for the moon and earth. by Thomas G. Barnes ICR Impact #110. 1982.
- How Long Would It Take the Moon to Recede from Earth to Its Present Position?
- The Moon is Still Young response to Tim Thompson’s “The Recession of the Moon” at Talk.Origins. rebutting Tim Thompson’s “The Recession of the Moon” at Talk.Origins). by Malcolm Bowden.
- Lunar Recession and the Slowing of the Earth's Rotation By Charles Creager Jr Which goes shows the math be involved in Lunar Recession.
- The Slowing of Earth Rotation and Lunar Recession By Charles Creager Jr Which including video one of which shows the math be involved in Lunar Recession and an interactive program that runs the calculation.