Fractal geometry
Fractal gemoetry, specifically the word fractal was coined by Benoît Mandelbrot in 1975 to describe geometric shapes that are "self-similar" -- that is, shapes that look the same at different magnifications, and which have fractional dimensions. Fractal shapes represent mathematical equations, and are produced by mathematicians using algorithms which perform the process of iteration or recursive sub-division. This process can go on infinitely, therefore, a fractal can have infinite resolution.
Fractal Creation
Fractals have been used for illustrating the regular features of complex objects and patterns. To create a fractal, start with a simple shape and duplicate it successively according to a set of fixed rules. Such a simple formula produce very complex structures, some of which have a striking resemblance to objects that appear in the real world. Natural phenomena such as the formation of snowflakes, clouds, mountain ranges, and landscapes involve patterns that are frequently not obvious to the naked eye. Their pictorial representations are fractals and are generated by computers using fractal geometry.
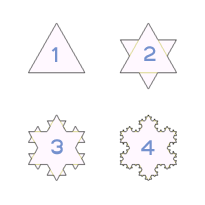
One of the simplest fractal shapes is generated by the process of iteration or recursive sub-division, and is known as the Koch curve or snowflake curve, which is pictured at right. The geometric operation consists of dividing a line into three equal parts and replacing the center section by two sides of an equilateral triangle. By repeating this operation again and again on smaller and smaller scales, a jagged snowflake is created.
It should be noted that although a fractal has statistical self-similarity at all resolutions if generated by an infinitely recursive process, in reality, those fractals generated by finite processes may exhibit no visible change in detail after some stage and so are adequate approximations.

Related References
- Fractal by Wikipedia
| ||||||||||||||||||||